Automata Tutorial

Theory of automata is a theoretical branch of computer science and mathematical. It is the study of abstract machines and the computation problems that can be solved using these machines. The abstract machine is called the automata. An automaton with a finite number of states is called a Finite automaton.

In this tutorial, we are going to learn how to construct deterministic finite automata, non-deterministic finite automata, Regular expression, context-free grammar, context-free language, Push down automata, Turning machines, etc.

Prerequisite

Before learning Automata, you should have a basic understanding of string, language, alphabets, symbols.

Audience

Our Automata Tutorial is designed to help beginners and professionals.

Problems

We assure that you will not find any problem in this Automata Tutorial. But if there is any mistake, please post the problem in contact form.

Theory of Automata

Theory of automata is a theoretical branch of computer science and mathematical. It is the study of abstract machines and the computation problems that can be solved using these machines. The abstract machine is called the automata. The main motivation behind developing the automata theory was to develop methods to describe and analyse the dynamic behaviour of discrete systems. 

This automaton consists of states and transitions. The State is represented by circles, and the Transitions is represented by arrows.

Automata is the kind of machine which takes some string as input and this input goes through a finite number of states and may enter in the final state.

There are the basic terminologies that are important and frequently used in automata:

Symbols:

Symbols are an entity or individual objects, which can be any letter, alphabet or any picture.

Example:

1, a, b, # 

Alphabets:

Alphabets are a finite set of symbols. It is denoted by ∑.

Examples:

String:

It is a finite collection of symbols from the alphabet. The string is denoted by w.

Example 1:

If ∑ = {a, b}, various string that can be generated from ∑ are {ab, aa, aaa, bb, bbb, ba, aba.....}.

• A string with zero occurrences of symbols is known as an empty string. It is represented by ε.
• The number of symbols in a string w is called the length of a string. It is denoted by |w|.

Example 2:

Language:

A language is a collection of appropriate string. A language which is formed over Σ can be Finite or Infinite.

Example: 1

L1 = {Set of string of length 2}

     = {aa, bb, ba, bb}          Finite Language

Example: 2

L2 = {Set of all strings starts with 'a'}

     = {a, aa, aaa, abb, abbb, ababb}         Infinite Language

Finite Automata

• Finite automata are used to recognize patterns.
• It takes the string of symbol as input and changes its state accordingly. When the desired symbol is found, then the transition occurs.
• At the time of transition, the automata can either move to the next state or stay in the same state.
• Finite automata have two states, Accept state or Reject state. When the input string is processed successfully, and the automata reached its final state, then it will accept.

Formal Definition of FA

A finite automaton is a collection of 5-tuple (Q, ∑, δ, q0, F), where:

1. Q: finite set of states  
2. ∑: finite set of the input symbol  
3. q0: initial state   
4. F: final state  
5. δ: Transition function  

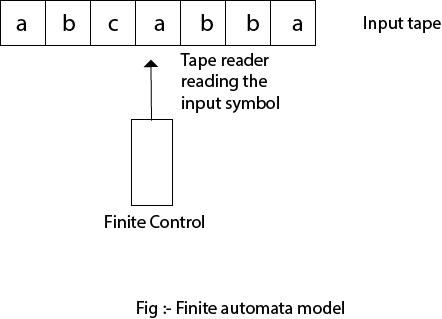
Finite Automata Model:

Finite automata can be represented by input tape and finite control.

Input tape: It is a linear tape having some number of cells. Each input symbol is placed in each cell.

Finite control: The finite control decides the next state on receiving particular input from input tape. The tape reader reads the cells one by one from left to right, and at a time only one input symbol is read.

Types of Automata:

There are two types of finite automata:

1. DFA(deterministic finite automata)
2. NFA(non-deterministic finite automata)

1. DFA

DFA refers to deterministic finite automata. Deterministic refers to the uniqueness of the computation. In the DFA, the machine goes to one state only for a particular input character. DFA does not accept the null move.

2. NFA

NFA stands for non-deterministic finite automata. It is used to transmit any number of states for a particular input. It can accept the null move.

Some important points about DFA and NFA:

1. Every DFA is NFA, but NFA is not DFA.
2. There can be multiple final states in both NFA and DFA.
3. DFA is used in Lexical Analysis in Compiler.
4. NFA is more of a theoretical concept.

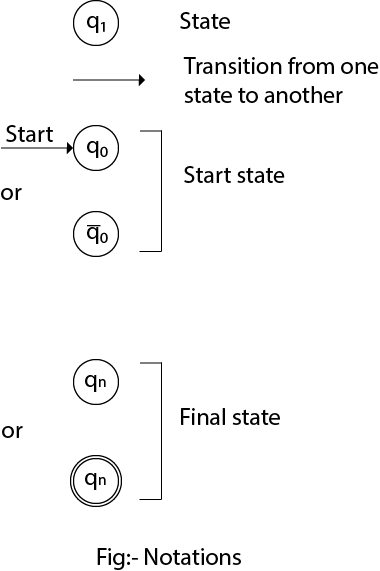
Transition Diagram

A transition diagram or state transition diagram is a directed graph which can be constructed as follows:

• There is a node for each state in Q, which is represented by the circle.
• There is a directed edge from node q to node p labeled a if δ(q, a) = p.
• In the start state, there is an arrow with no source.
• Accepting states or final states are indicating by a double circle.

Some Notations that are used in the transition diagram:

There is a description of how a DFA operates:

1. In DFA, the input to the automata can be any string. Now, put a pointer to the start state q and read the input string w from left to right and move the pointer according to the transition function, δ. We can read one symbol at a time. If the next symbol of string w is a and the pointer is on state p, move the pointer to δ(p, a). When the end of the input string w is encountered, then the pointer is on some state F.

2. The string w is said to be accepted by the DFA if r ∈ F that means the input string w is processed successfully and the automata reached its final state. The string is said to be rejected by DFA if r ∉ F.

Example 1:

DFA with ∑ = {0, 1} accepts all strings starting with 1.

Solution:

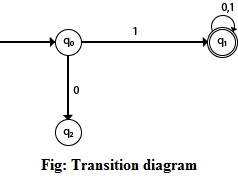
The finite automata can be represented using a transition graph. In the above diagram, the machine initially is in start state q0 then on receiving input 1 the machine changes its state to q1. From q0 on receiving 0, the machine changes its state to q2, which is the dead state. From q1 on receiving input 0, 1 the machine changes its state to q1, which is the final state. The possible input strings that can be generated are 10, 11, 110, 101, 111......., that means all string starts with 1.

Example 2:

NFA with ∑ = {0, 1} accepts all strings starting with 1.

Solution:

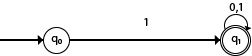
The NFA can be represented using a transition graph. In the above diagram, the machine initially is in start state q0 then on receiving input 1 the machine changes its state to q1. From q1 on receiving input 0, 1 the machine changes its state to q1. The possible input string that can be generated is 10, 11, 110, 101, 111......, that means all string starts with 1.

Transition Table

The transition table is basically a tabular representation of the transition function. It takes two arguments (a state and a symbol) and returns a state (the "next state").

A transition table is represented by the following things:

• Columns correspond to input symbols.
• Rows correspond to states.
• Entries correspond to the next state.
• The start state is denoted by an arrow with no source.
• The accept state is denoted by a star. 

Example 1:

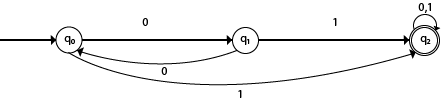
Solution:

Transition table of given DFA is as follows:

Present State	Next state for Input 0	Next State of Input 1
→q0	q1	q2
q1	q0	q2
*q2	q2	q2

Explanation:

• In the above table, the first column indicates all the current states. Under column 0 and 1, the next states are shown.
• The first row of the transition table can be read as, when the current state is q0, on input 0 the next state will be q1 and on input 1 the next state will be q2.
• In the second row, when the current state is q1, on input 0, the next state will be q0, and on 1 input the next state will be q2.
• In the third row, when the current state is q2 on input 0, the next state will be q2, and on 1 input the next state will be q2.
• The arrow marked to q0 indicates that it is a start state and circle marked to q2 indicates that it is a final state.

Example 2:

Solution:

Transition table of given NFA is as follows:

Present State	Next state for Input 0	Next State of Input 1
→q0	q0	q1
q1	q1, q2	q2
q2	q1	q3
*q3	q2	q2

Explanation:

• The first row of the transition table can be read as, when the current state is q0, on input 0 the next state will be q0 and on input 1 the next state will be q1.
• In the second row, when the current state is q1, on input 0 the next state will be either q1 or q2, and on 1 input the next state will be q2.
• In the third row, when the current state is q2 on input 0, the next state will be q1, and on 1 input the next state will be q3.
• In the fourth row, when the current state is q3 on input 0, the next state will be q2, and on 1 input the next state will be q2.

---