Concepts, Conversion and Minimization Of DFA & NFA
DFA (Deterministic finite automata)
- DFA refers to deterministic finite automata. Deterministic refers to the uniqueness of the computation. The finite automata are called deterministic finite automata if the machine is read an input string one symbol at a time.
- In DFA, there is only one path for specific input from the current state to the next state.
- DFA does not accept the null move, i.e., the DFA cannot change state without any input character.
- DFA can contain multiple final states. It is used in Lexical Analysis in Compiler.
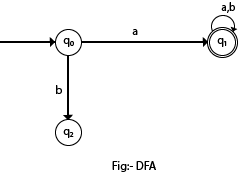
In the following diagram, we can see that from state q0 for input a, there is only one path which is going to q1. Similarly, from q0, there is only one path for input b going to q2.
Formal Definition of DFA
A DFA is a collection of 5-tuples same as we described in the definition of FA.
Transition function can be defined as:
Graphical Representation of DFA
A DFA can be represented by digraphs called state diagram. In which:
- The state is represented by vertices.
- The arc labeled with an input character show the transitions.
- The initial state is marked with an arrow.
- The final state is denoted by a double circle.
Example 1:
Solution:
Transition Diagram:

Transition Table:
| Present State | Next state for Input 0 | Next State of Input 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | q2 | q1 |
| *q2 | q2 | q2 |
Example 2:
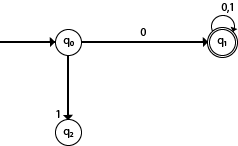
DFA with ∑ = {0, 1} accepts all starting with 0.
Solution:
Explanation:
- In the above diagram, we can see that on given 0 as input to DFA in state q0 the DFA changes state to q1 and always go to final state q1 on starting input 0. It can accept 00, 01, 000, 001....etc. It can't accept any string which starts with 1, because it will never go to final state on a string starting with 1.
Example 3:
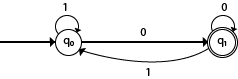
DFA with ∑ = {0, 1} accepts all ending with 0.
Solution:
Explanation:
In the above diagram, we can see that on given 0 as input to DFA in state q0, the DFA changes state to q1. It can accept any string which ends with 0 like 00, 10, 110, 100....etc. It can't accept any string which ends with 1, because it will never go to the final state q1 on 1 input, so the string ending with 1, will not be accepted or will be rejected.
Examples of DFA
Example 1:
Design a FA with ∑ = {0, 1} accepts those string which starts with 1 and ends with 0.
Solution:
The FA will have a start state q0 from which only the edge with input 1 will go to the next state.

In state q1, if we read 1, we will be in state q1, but if we read 0 at state q1, we will reach to state q2 which is the final state. In state q2, if we read either 0 or 1, we will go to q2 state or q1 state respectively. Note that if the input ends with 0, it will be in the final state.
Example 2:
Design a FA with ∑ = {0, 1} accepts the only input 101.
Solution:

In the given solution, we can see that only input 101 will be accepted. Hence, for input 101, there is no other path shown for other input.
Example 3:
Design FA with ∑ = {0, 1} accepts even number of 0's and even number of 1's.
Solution:
This FA will consider four different stages for input 0 and input 1. The stages could be:
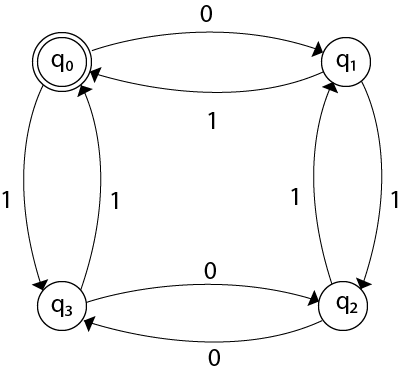
Here q0 is a start state and the final state also. Note carefully that a symmetry of 0's and 1's is maintained. We can associate meanings to each state as:
q0: state of even number of 0's and even number of 1's.
q1: state of odd number of 0's and even number of 1's.
q2: state of odd number of 0's and odd number of 1's.
q3: state of even number of 0's and odd number of 1's.
Example 4:
Design FA with ∑ = {0, 1} accepts the set of all strings with three consecutive 0's.
Solution:
The strings that will be generated for this particular languages are 000, 0001, 1000, 10001, .... in which 0 always appears in a clump of 3. The transition graph is as follows:
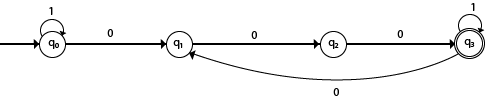
Note that the sequence of triple zeros is maintained to reach the final state.
Example 5:
Design a DFA L(M) = {w | w ε {0, 1}*} and W is a string that does not contain consecutive 1's.
Solution:
When three consecutive 1's occur the DFA will be:
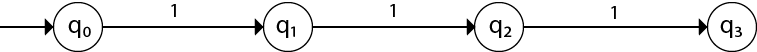
Here two consecutive 1's or single 1 is acceptable, hence

The stages q0, q1, q2 are the final states. The DFA will generate the strings that do not contain consecutive 1's like 10, 110, 101,..... etc.
Example 6:
Design a FA with ∑ = {0, 1} accepts the strings with an even number of 0's followed by single 1.
Solution:
The DFA can be shown by a transition diagram as:
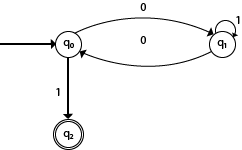
NFA (Non-Deterministic finite automata)
- NFA stands for non-deterministic finite automata. It is easy to construct an NFA than DFA for a given regular language.
- The finite automata are called NFA when there exist many paths for specific input from the current state to the next state.
- Every NFA is not DFA, but each NFA can be translated into DFA.
- NFA is defined in the same way as DFA but with the following two exceptions, it contains multiple next states, and it contains ε transition.
In the following image, we can see that from state q0 for input a, there are two next states q1 and q2, similarly, from q0 for input b, the next states are q0 and q1. Thus it is not fixed or determined that with a particular input where to go next. Hence this FA is called non-deterministic finite automata.
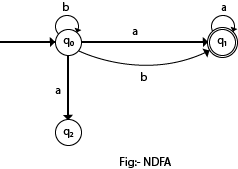
Formal definition of NFA:
NFA also has five states same as DFA, but with different transition function, as shown follows:
δ: Q x ∑ →2Q
where,
Graphical Representation of an NFA
An NFA can be represented by digraphs called state diagram. In which:
- The state is represented by vertices.
- The arc labeled with an input character show the transitions.
- The initial state is marked with an arrow.
- The final state is denoted by the double circle.
Example 1:
Solution:
Transition diagram:
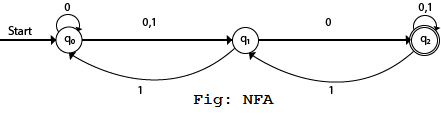
Transition Table:
| Present State | Next state for Input 0 | Next State of Input 1 |
|---|---|---|
| →q0 | q0, q1 | q1 |
| q1 | q2 | q0 |
| *q2 | q2 | q1, q2 |
In the above diagram, we can see that when the current state is q0, on input 0, the next state will be q0 or q1, and on 1 input the next state will be q1. When the current state is q1, on input 0 the next state will be q2 and on 1 input, the next state will be q0. When the current state is q2, on 0 input the next state is q2, and on 1 input the next state will be q1 or q2.
Example 2:
NFA with ∑ = {0, 1} accepts all strings with 01.
Solution:

Transition Table:
| Present State | Next state for Input 0 | Next State of Input 1 |
|---|---|---|
| →q0 | q1 | ε |
| q1 | ε | q2 |
| *q2 | q2 | q2 |
Example 3:
NFA with ∑ = {0, 1} and accept all string of length atleast 2.
Solution:
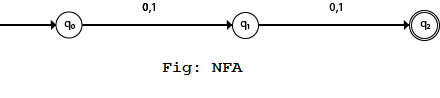
Transition Table:
| Present State | Next state for Input 0 | Next State of Input 1 |
|---|---|---|
| →q0 | q1 | q1 |
| q1 | q2 | q2 |
| *q2 | ε | ε |
Examples of NFA
Example 1:
Design a NFA for the transition table as given below:
| Present State | 0 | 1 |
|---|---|---|
| →q0 | q0, q1 | q0, q2 |
| q1 | q3 | ε |
| q2 | q2, q3 | q3 |
| →q3 | q3 | q3 |
Solution:
The transition diagram can be drawn by using the mapping function as given in the table.
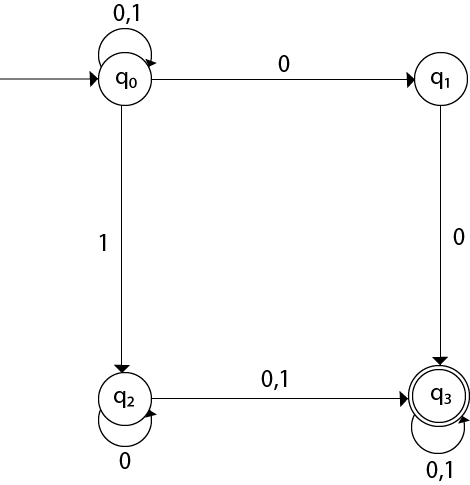
Here,
Example 2:
Design an NFA with ∑ = {0, 1} accepts all string ending with 01.
Solution:

Hence, NFA would be:

Example 3:
Design an NFA with ∑ = {0, 1} in which double '1' is followed by double '0'.
Solution:
The FA with double 1 is as follows:

It should be immediately followed by double 0.
Then,

Now before double 1, there can be any string of 0 and 1. Similarly, after double 0, there can be any string of 0 and 1.
Hence the NFA becomes:

Now considering the string 01100011
Example 4:
Design an NFA in which all the string contain a substring 1110.
Solution:
The language consists of all the string containing substring 1010. The partial transition diagram can be:

Now as 1010 could be the substring. Hence we will add the inputs 0's and 1's so that the substring 1010 of the language can be maintained. Hence the NFA becomes:

Transition table for the above transition diagram can be given below:
| Present State | 0 | 1 |
|---|---|---|
| →q1 | q1 | q1, q2 |
| q2 | q3 | |
| q3 | q4 | |
| q4 | q5 | |
| *q5 | q5 | q5 |
Consider a string 111010,
Got stuck! As there is no path from q2 for input symbol 0. We can process string 111010 in another way.
As state q5 is the accept state. We get the complete scanned, and we reached to the final state.
Example 5:
Design an NFA with ∑ = {0, 1} accepts all string in which the third symbol from the right end is always 0.
Solution:

Thus we get the third symbol from the right end as '0' always. The NFA can be:

The above image is an NFA because in state q0 with input 0, we can either go to state q0 or q1.
Eliminating ε Transitions
NFA with ε can be converted to NFA without ε, and this NFA without ε can be converted to DFA. To do this, we will use a method, which can remove all the ε transition from given NFA. The method will be:
- Find out all the ε transitions from each state from Q. That will be called as ε-closure{q1} where qi ∈ Q.
- Then δ' transitions can be obtained. The δ' transitions mean a ε-closure on δ moves.
- Repeat Step-2 for each input symbol and each state of given NFA.
- Using the resultant states, the transition table for equivalent NFA without ε can be built.
Example:
Convert the following NFA with ε to NFA without ε.
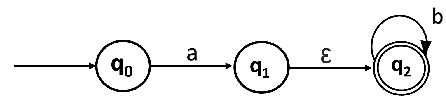
Solutions: We will first obtain ε-closures of q0, q1 and q2 as follows:
Now the δ' transition on each input symbol is obtained as:
Now the δ' transition on q1 is obtained as:
- δ'(q1, a) = ε-closure(δ(δ^(q1, ε),a))
- = ε-closure(δ(ε-closure(q1),a))
- = ε-closure(δ(q1, q2), a)
- = ε-closure(δ(q1, a) ∪ δ(q2, a))
- = ε-closure(Ф ∪ Ф)
- = Ф
- δ'(q1, b) = ε-closure(δ(δ^(q1, ε),b))
- = ε-closure(δ(ε-closure(q1),b))
- = ε-closure(δ(q1, q2), b)
- = ε-closure(δ(q1, b) ∪ δ(q2, b))
- = ε-closure(Ф ∪ q2)
- = {q2}
The δ' transition on q2 is obtained as:
Now we will summarize all the computed δ' transitions:
The transition table can be:
| States | a | b |
|---|---|---|
| →q0 | {q1, q2} | Ф |
| *q1 | Ф | {q2} |
| *q2 | Ф | {q2} |
State q1 and q2 become the final state as ε-closure of q1 and q2 contain the final state q2. The NFA can be shown by the following transition diagram:
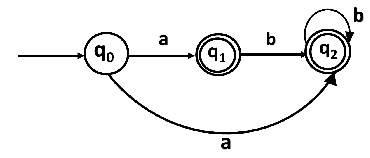
Conversion from NFA to DFA
In this section, we will discuss the method of converting NFA to its equivalent DFA. In NFA, when a specific input is given to the current state, the machine goes to multiple states. It can have zero, one or more than one move on a given input symbol. On the other hand, in DFA, when a specific input is given to the current state, the machine goes to only one state. DFA has only one move on a given input symbol.
Let, M = (Q, ∑, δ, q0, F) is an NFA which accepts the language L(M). There should be equivalent DFA denoted by M' = (Q', ∑', q0', δ', F') such that L(M) = L(M').
Steps for converting NFA to DFA:
Step 1: Initially Q' = ϕ
Step 2: Add q0 of NFA to Q'. Then find the transitions from this start state.
Step 3: In Q', find the possible set of states for each input symbol. If this set of states is not in Q', then add it to Q'.
Step 4: In DFA, the final state will be all the states which contain F(final states of NFA)
Example 1:
Convert the given NFA to DFA.
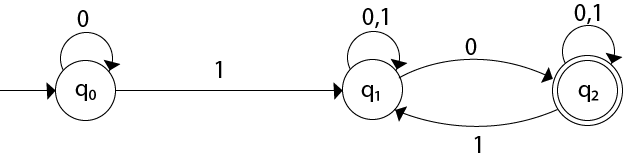
Solution: For the given transition diagram we will first construct the transition table.
| State | 0 | 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | {q1, q2} | q1 |
| *q2 | q2 | {q1, q2} |
Now we will obtain δ' transition for state q0.
The δ' transition for state q1 is obtained as:
The δ' transition for state q2 is obtained as:
Now we will obtain δ' transition on [q1, q2].
The state [q1, q2] is the final state as well because it contains a final state q2. The transition table for the constructed DFA will be:
| State | 0 | 1 |
|---|---|---|
| →[q0] | [q0] | [q1] |
| [q1] | [q1, q2] | [q1] |
| *[q2] | [q2] | [q1, q2] |
| *[q1, q2] | [q1, q2] | [q1, q2] |
The Transition diagram will be:
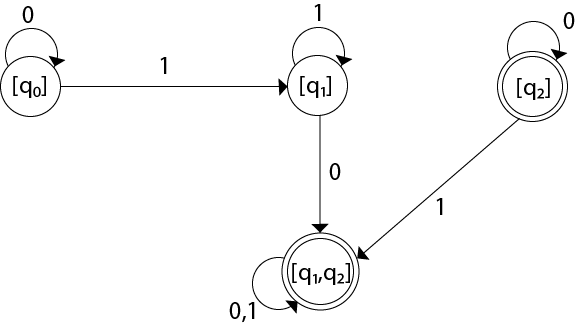
The state q2 can be eliminated because q2 is an unreachable state.
Example 2:
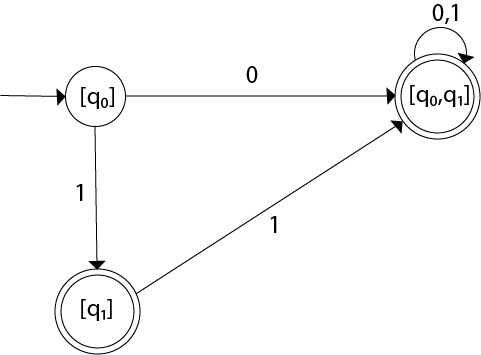
Convert the given NFA to DFA.
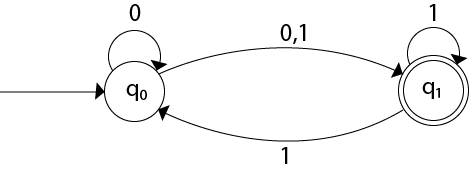
Solution: For the given transition diagram we will first construct the transition table.
| State | 0 | 1 |
|---|---|---|
| →q0 | {q0, q1} | {q1} |
| *q1 | ϕ | {q0, q1} |
Now we will obtain δ' transition for state q0.
The δ' transition for state q1 is obtained as:
Now we will obtain δ' transition on [q0, q1].
Similarly,
As in the given NFA, q1 is a final state, then in DFA wherever, q1 exists that state becomes a final state. Hence in the DFA, final states are [q1] and [q0, q1]. Therefore set of final states F = {[q1], [q0, q1]}.
The transition table for the constructed DFA will be:
| State | 0 | 1 |
|---|---|---|
| →[q0] | [q0, q1] | [q1] |
| *[q1] | ϕ | [q0, q1] |
| *[q0, q1] | [q0, q1] | [q0, q1] |
The Transition diagram will be:
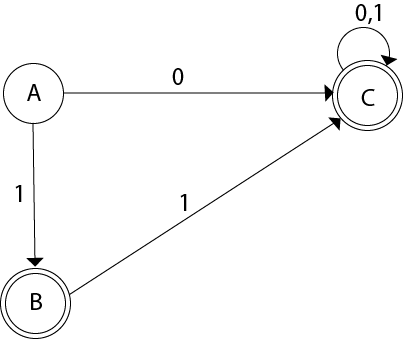
Even we can change the name of the states of DFA.
Suppose
With these new names the DFA will be as follows:
Conversion from NFA with ε to DFA
Non-deterministic finite automata(NFA) is a finite automata where for some cases when a specific input is given to the current state, the machine goes to multiple states or more than 1 states. It can contain ε move. It can be represented as M = { Q, ∑, δ, q0, F}.
Where
NFA with ∈ move: If any FA contains ε transaction or move, the finite automata is called NFA with ∈ move.
ε-closure: ε-closure for a given state A means a set of states which can be reached from the state A with only ε(null) move including the state A itself.
Steps for converting NFA with ε to DFA:
Step 1: We will take the ε-closure for the starting state of NFA as a starting state of DFA.
Step 2: Find the states for each input symbol that can be traversed from the present. That means the union of transition value and their closures for each state of NFA present in the current state of DFA.
Step 3: If we found a new state, take it as current state and repeat step 2.
Step 4: Repeat Step 2 and Step 3 until there is no new state present in the transition table of DFA.
Step 5: Mark the states of DFA as a final state which contains the final state of NFA.
Example 1:
Convert the NFA with ε into its equivalent DFA.
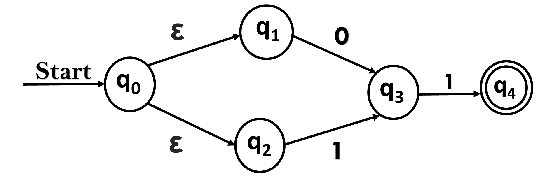
Solution:
Let us obtain ε-closure of each state.
Now, let ε-closure {q0} = {q0, q1, q2} be state A.
Hence
δ'(A, 0) = ε-closure {δ((q0, q1, q2), 0) }
= ε-closure {δ(q0, 0) ∪ δ(q1, 0) ∪ δ(q2, 0) }
= ε-closure {q3}
= {q3} call it as state B.
δ'(A, 1) = ε-closure {δ((q0, q1, q2), 1) }
= ε-closure {δ((q0, 1) ∪ δ(q1, 1) ∪ δ(q2, 1) }
= ε-closure {q3}
= {q3} = B.
The partial DFA will be
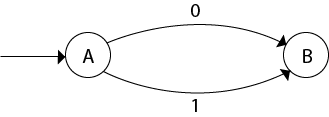
Now,
δ'(B, 0) = ε-closure {δ(q3, 0) }
= ϕ
δ'(B, 1) = ε-closure {δ(q3, 1) }
= ε-closure {q4}
= {q4} i.e. state C
For state C:
The DFA will be,
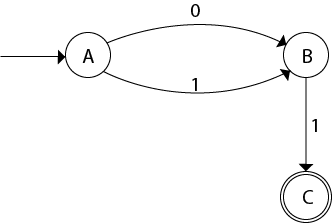
Example 2:
Convert the given NFA into its equivalent DFA.
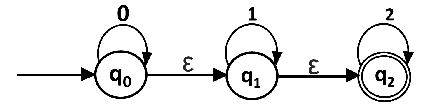
Solution: Let us obtain the ε-closure of each state.
Now we will obtain δ' transition. Let ε-closure(q0) = {q0, q1, q2} call it as state A.
δ'(A, 0) = ε-closure{δ((q0, q1, q2), 0)}
= ε-closure{δ(q0, 0) ∪ δ(q1, 0) ∪ δ(q2, 0)}
= ε-closure{q0}
= {q0, q1, q2}
δ'(A, 1) = ε-closure{δ((q0, q1, q2), 1)}
= ε-closure{δ(q0, 1) ∪ δ(q1, 1) ∪ δ(q2, 1)}
= ε-closure{q1}
= {q1, q2} call it as state B
δ'(A, 2) = ε-closure{δ((q0, q1, q2), 2)}
= ε-closure{δ(q0, 2) ∪ δ(q1, 2) ∪ δ(q2, 2)}
= ε-closure{q2}
= {q2} call it state C
Thus we have obtained
The partial DFA will be:
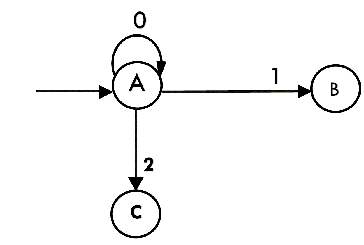
Now we will find the transitions on states B and C for each input.
Hence
δ'(B, 0) = ε-closure{δ((q1, q2), 0)}
= ε-closure{δ(q1, 0) ∪ δ(q2, 0)}
= ε-closure{ϕ}
= ϕ
δ'(B, 1) = ε-closure{δ((q1, q2), 1)}
= ε-closure{δ(q1, 1) ∪ δ(q2, 1)}
= ε-closure{q1}
= {q1, q2} i.e. state B itself
δ'(B, 2) = ε-closure{δ((q1, q2), 2)}
= ε-closure{δ(q1, 2) ∪ δ(q2, 2)}
= ε-closure{q2}
= {q2} i.e. state C itself
Thus we have obtained
The partial transition diagram will be
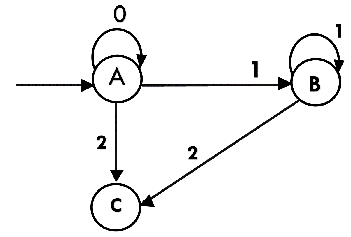
Now we will obtain transitions for C:
δ'(C, 0) = ε-closure{δ(q2, 0)}
= ε-closure{ϕ}
= ϕ
δ'(C, 1) = ε-closure{δ(q2, 1)}
= ε-closure{ϕ}
= ϕ
δ'(C, 2) = ε-closure{δ(q2, 2)}
= {q2}
Hence the DFA is
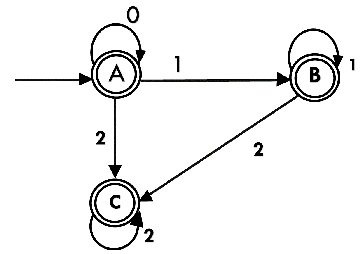
As A = {q0, q1, q2} in which final state q2 lies hence A is final state. B = {q1, q2} in which the state q2 lies hence B is also final state. C = {q2}, the state q2 lies hence C is also a final state.
Minimization of DFA
Minimization of DFA means reducing the number of states from given FA. Thus, we get the FSM(finite state machine) with redundant states after minimizing the FSM.
We have to follow the various steps to minimize the DFA. These are as follows:
Step 1: Remove all the states that are unreachable from the initial state via any set of the transition of DFA.
Step 2: Draw the transition table for all pair of states.
Step 3: Now split the transition table into two tables T1 and T2. T1 contains all final states, and T2 contains non-final states.
Step 4: Find similar rows from T1 such that:
That means, find the two states which have the same value of a and b and remove one of them.
Step 5: Repeat step 3 until we find no similar rows available in the transition table T1.
Step 6: Repeat step 3 and step 4 for table T2 also.
Step 7: Now combine the reduced T1 and T2 tables. The combined transition table is the transition table of minimized DFA.
Example:
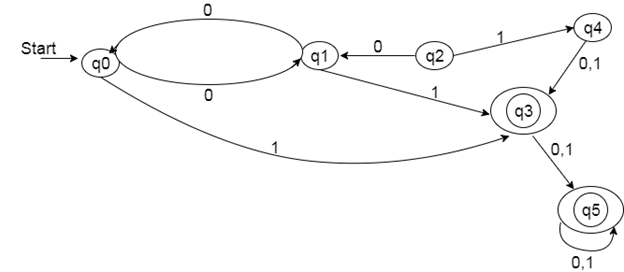
Solution:
Step 1: In the given DFA, q2 and q4 are the unreachable states so remove them.
Step 2: Draw the transition table for the rest of the states.
| State | 0 | 1 |
|---|---|---|
| →q0 | q1 | q3 |
| q1 | q0 | q3 |
| *q3 | q5 | q5 |
| *q5 | q5 | q5 |
Step 3: Now divide rows of transition table into two sets as:
1. One set contains those rows, which start from non-final states:
| State | 0 | 1 |
|---|---|---|
| q0 | q1 | q3 |
| q1 | q0 | q3 |
2. Another set contains those rows, which starts from final states.
| State | 0 | 1 |
|---|---|---|
| q3 | q5 | q5 |
| q5 | q5 | q5 |
Step 4: Set 1 has no similar rows so set 1 will be the same.
Step 5: In set 2, row 1 and row 2 are similar since q3 and q5 transit to the same state on 0 and 1. So skip q5 and then replace q5 by q3 in the rest.
| State | 0 | 1 |
|---|---|---|
| q3 | q3 | q3 |
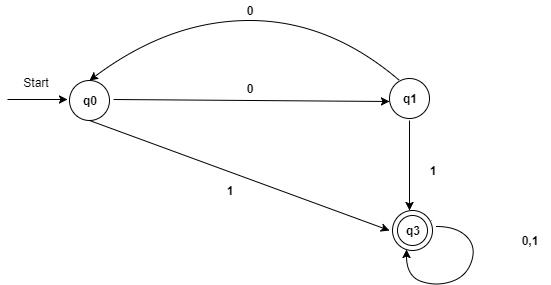
Step 6: Now combine set 1 and set 2 as:
| State | 0 | 1 |
|---|---|---|
| →q0 | q1 | q3 |
| q1 | q0 | q3 |
| *q3 | q3 | q3 |
Now it is the transition table of minimized DFA.


2 comments